元の職場で話題提供のために作ったコンテンツです。元ネタはこちらになります。
130 年前にアイルランドの市井の土木技術者が晩年に書いた一遍の論文で記載した近似式が全世界的に使われるようになった、という話です。

年 譜
先ずは Manning さんの生涯の主な出来事です。
ほぼ、勝海舟(1823-1899)と同じ時代の人、ということになります。
| 年 | 歳 | 出来事 |
|---|---|---|
| 1816.10.22 | 0 | 父親の任地、ノルマンディー (仏) にて誕生 |
| 1826 | 10 | ウォーターフォード (アイルランド) に移住 |
| ? | 会計士として就職 | |
| 1846 | 30 | アイルランド公共事業局幹線排水課に製図工として転職 |
| その後、同局のサミュエル・ロバートのアシスタントに就く | ||
| 1848-55 | 32-39 | 同課にて地区の技師に昇格 |
| この間にダビュイソンの著書と出会い水理学に目覚める | ||
| 1855-69 | 39-50 | ダウンシャー公爵に雇われてダウンドラム築港の現場監督に就く |
| ベルファストの配水事業にも従事 | ||
| 1869 (明治2年) | 50 | 技師長補佐としてアイルランド公共事業局に復職 |
| 1874 | 58 | 技師長に昇格 |
| 1889.12.4 | 73 | アイルランド土木学会に論文を提出 |
| 1891 | 75 | アイルランド公共事業局退職。論文が学会誌に掲載される |
| 1897.12.9 | 81 | ダブリンにて永眠 |
オリジナルのマニング式
- 流体力学・水理学に関する教育も正規の訓練も受けていない彼にとって実務をこなすための簡易式が必要であった
- そこで、当時著名であった 7 種類の流速公式 (Du Buat, Eyelwein, Weisbach, St. Venant, Neville, Darcy and Bazin, Ganguillet and Kutter) を用いて、勾配と径深を変えた時の流速を計算して比較
- 先ず 7 式の平均値の近似式として \(V=32\bigl[ RS(1+R^{1/3})\bigr]^{1/2}\)
- これを簡単化して \(V=CR^x S^{1/2}\)
- そして、1885年には \(C\) は Ganguillet and Kutter の \(n\) の逆数とほぼ等価、として
$$V=CR^{2/3} S^{1/2}$$ - つまり、今日、我々が「マニングの祖度係数」としている係数は次の Ganguillet and Kutter 式中の定数。
$$
V = \frac{\displaystyle{23+\frac{1}{n}+\frac{0.00155}{S}}\vphantom{\int}}
{\displaystyle{1 + \left( 23 + \frac{0.00155}{S}\right)\frac{n}{\sqrt{R}}}\vphantom{\int}}
\sqrt{RS}
$$
その後
- 当時、立方根の計算が面倒であったこと、\(n\) が無次元でないことが不満だったので、彼の提案した最終形は下式であった
$$
V = C’\sqrt{gS}\left[\sqrt{R}+\frac{0.22(R – 0.15 m)}{\sqrt{m}}\right]
$$
- 1918 年にキング博士 (ミシガン大) が監修した「水工学ハンドブック」に今日知られている次式が紹介されたことで普及し、一部の教科書にも掲載された
$$
V=\frac{1}{n}R^{2/3} \sqrt{S}
$$
- ちなみに Wikipedia によれば、マニングに先んじること 23 年前の 1867年 にゴクレール (仏) が同様の式を発表していた模様で、ヨーロッパでは「ゴクレール・マニング・ストリクラー式」と呼ばれている由
余 話
「年譜」で記したように Manning さんはダビュイソン(d‘Aubisson des Voissons 仏 1769-1841)の著書にふれて水理学に目覚めた。
ダビュイソンが提案した次の橋脚による堰上げの推定式は未だに本邦の技術マニュアルに掲載されている
$$
h= \frac{\alpha Q^2}{2g}\left[
\left\{\frac{1}{\mu(B – a)H_3} \right\}^{2}-
\left\{\frac{1}{B(H_3 + h)} \right\}^{2}
\right]$$
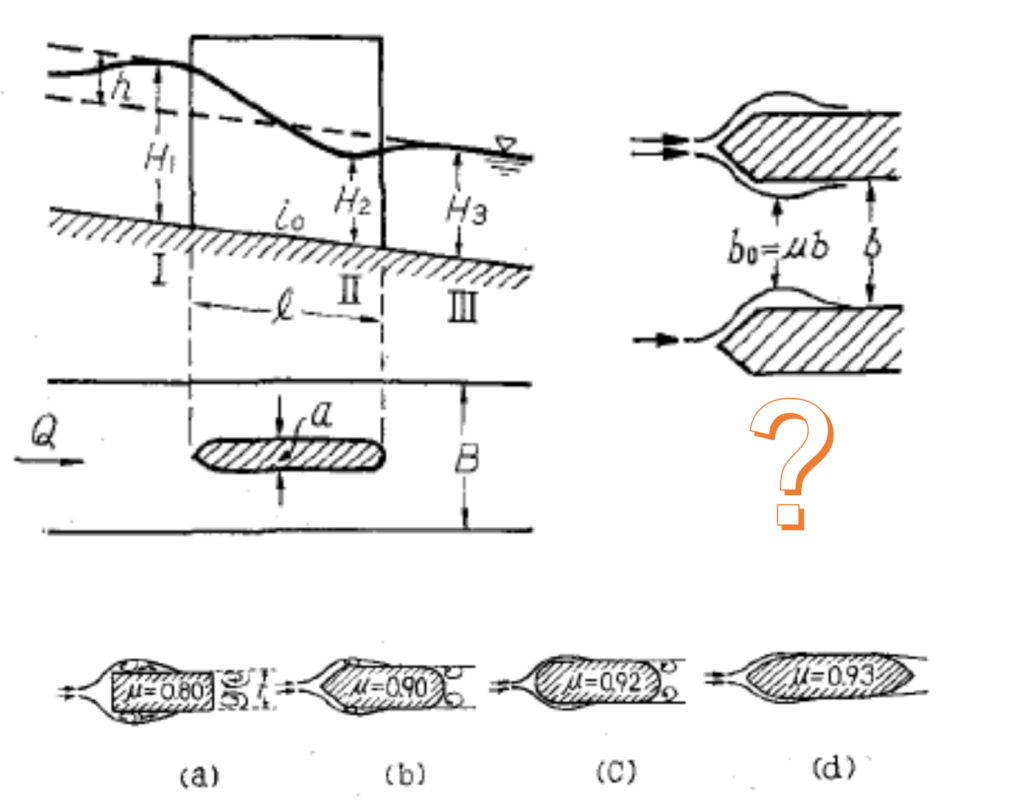
が・・・。この式は
摩擦損失なし、上図で \(H_2 =H_3\)、橋脚の形状別の縮流を仮定して、\(\mbox{I – II -III}\) の運動量の保存を考えた (だけ)
のもので、明らかに矩形の小水路限定。そうでないと、剥離渦のサイズが橋脚の間隔に依存するものになって低水路内の橋脚も堤防際の高水敷の橋脚も同じ抵抗になってしまう。むやみに使っちゃダメっしょ。