今回は合理式の話です。発案者はエミル・クイヒリング(Emil Kuichling 独 1848-1914)です。前回の Manning さんより 30 歳ほど若い人です。

キャリア
1868 ロチェスター大学 (NY) 卒
1873-1900 ロチェスター市水道局 1890- 技師長
ロチェスター科学アカデミー会頭 ASCE 副会長
合理式の起源
- 初出は The relation between the rainfall and the discharge of sewers in populous districts. Trans. ASCE 20: 1-60.1889
$$
Q_p = C \cdot i \cdot A
$$
- 論文名の通り都市域の雨水排水が対象
- 定式化には至らなかったものの、基本的なアイデアは 1851 年にアイルランドのマルヴァネイという人が提示していた模様
- 若干、遅れて ロイド・デーヴィス(英)も 1905 年に現在用いらている次式(実際は単位系・流出率の表現が異なる)を提案した
$$
Q_p = \frac{1}{3.6} \cdot f \cdot r \cdot A
$$
- 何時 「合理式(ラショナル式)」 と称せられるようになったか、は不明であるが、1932 年の ASCE の論文集には、先人の偉大な業績である 「so called rational method」 なる記載がある
- 我が国では
- 1914 年に物部長穂が成書「水理学」で「最大流出量の算定式」として紹介。出典を明らかにしなかったので、以後「物部公式」とされた(確信犯?)
- 1915 年に東京府下水道改良事務所の米元晋一がロイド・デーヴィスの論文を「合理的計算法」として引用
合理式は合理的か
- 石原・高棹らは下図のように洪水到達時間をとれば合理式が水理学的にも成立、つまり理論的に説明可能であることを示した
$$
Q_p = Q(t_2) = \frac{r_m A}{3.6}\quad
r_m = \frac{1}{t_p}\int_{t_1}^{t_2}\!\!r_e\,dt
$$
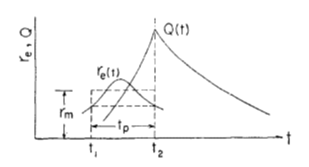
- ただし、有効降雨は空間的に一様、斜面勾配は一定、が前提なので、むやみに大きな集水域では適用できない
さらば (幻の) クラーヘン式
- 角屋らは前頁の方法で実流域の洪水到達時間と平均有効降雨強度の標本を作成し、洪水到達時間の推定式として次式を提案
$$
t_p = CA^{0.22}/r_m^{0.35}
$$
- しかるに、我国では洪水の伝播速度 \(W\) の推定に次の「Rziha の式」や「Kraven の式」を用いて洪水到達時間を計算していることが多い
$$
\begin{align*}&W = 20 \left( \frac{H}{L} \right)^{0.6}& \mbox{Rziha}\\&W = \begin{cases}3.5 & 1/100\le H/L \\3.0 & 1/200\le H/L < 1/100 \\2.1 & \hphantom{1/200\ge\,\,} H/L<1/200\end{cases}& \mbox{Kraven}\end{align*}
$$
- 井口昌平は 1957 年にこれらの由緒を追跡して
- Kraven の式なるものは存在せず、Kaven(Kraven ではない)の調査結果を Rziha が紹介したに過ぎない
- Rziha の式も「バイエルン地方でつかいならされている式」として彼が紹介しただけ。当国(独)での評判はよろしくない
- 結論は、何で日本で使われ出したのか皆目不明(物部長穂が「水理学」で紹介したから?)
平均降雨強度
- 下図は降雨観測所の降雨強度曲線と流域平均雨量のそれを比較したもの。年超過確率は 1/30。流域平均雨量は解析雨量を用いて推定
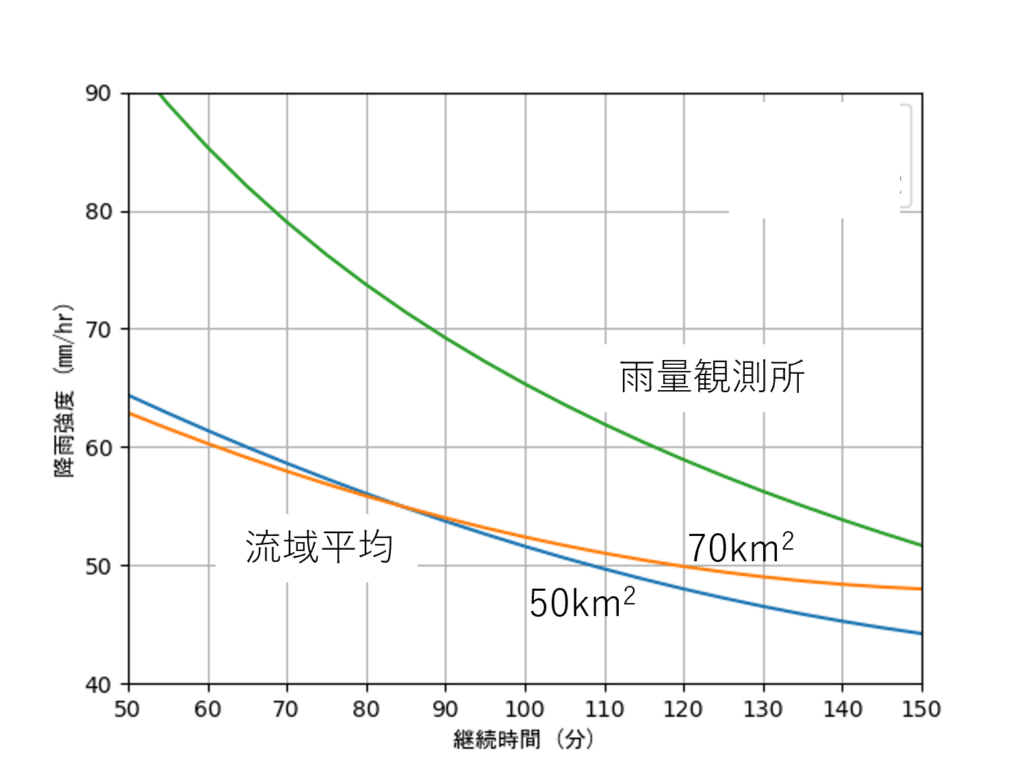
- 点雨量の極値は流域平均雨量のそれより大きいから当然の結果。したがって、点雨量の降雨強度式に依拠している中小河川の計画高水流量は過大評価となっている可能性が高い。ひいては超過洪水時に下流河川に過剰な負荷を与えることが懸念される
- そもそも論としては、適用範囲を超えて合理式を採用していることに拠る。アメリカの技術基準では 200エーカー (0.8 km2) を適用可能な集水域面積の上限としている
- 近年は中小河川においても水文観測体制が整ってきているので、きちんと降雨と流出の関係を見直す必要があるのではなかろうか
- ついでに言うと、ティーセンさんが提案した流域平均雨量の計算法は一世紀前の産物。いつまで使い続ける?