ふとしたキッカケがあって、鉛直一次元の不飽和浸透流についてお勉強した。
インターネットで色々調べていて、偶々、京大防災研 菅原快斗氏の『不飽和浸透流の解析手法と降雨流出モデルへの応用』という論文に行き当たった。第2章が「地下水面を有する土壌における Richards 式の解析解」となっており、興味深いので解析解の導出をトレースしてみた。
命題は次の Richards 式
$$
\frac{\partial S}{\partial t} = D\frac{\partial^2 S}{\partial z^2} –
V\frac{\partial S}{\partial z}
\raise{-12px}{,}\quad
D = \frac{k_s}{\alpha(\theta_s – \theta_r)}
\raise{-12px}{,}\quad
V = \frac{k_s}{\theta_s – \theta_r}
$$
を
$$
S(0, t) = S_U\,,\quad
S(L, t) = S_L\,,\quad
S(z, 0) = S_0(z)
$$
の元で解く、というものです。
ここに、\(t\):時間座標、\(z\):鉛直下方を正とする空間座標、\(S\):有効飽和度、\(\theta_s\):飽和体積含水率、\(\theta_r\):残留体積含水率、\(\alpha\):Gardner モデルで水分保持曲線の形状を決定するパラメータ、\(k_s\):飽和透水係数、です。
過程をスキップして、任意の座標での流量
$$
q = -\frac{k_s}{\alpha} \frac{\partial S}{\partial z} + k_s S
$$
は
$$
q =k_s B -k_s \sum_{n=1}^{\infty} \,l_n \cdot f_n
$$
$$
l_n = \frac{2}{L} \int_0^L \biggl[\bigl\{ S_0(z) – A \exp\left( \alpha z \right) – B\bigr\}\exp\left( -\frac{\alpha}{2} z \right) \sin\left( \frac{n \pi}{L} z \right)
\biggr] dz
$$
$$
f_n=\exp\left[-\left\{ \left( \frac{n \pi}{L}\right)^2 + \frac{\alpha^2}{4} \right\} D\,t + \frac{\alpha}{2} z \right] \left[\frac{1}{2}\sin\left( \frac{n \pi}{L} z\right) +\frac{n \pi}{\alpha L} \cos\left( \frac{n \pi}{L} z\right)\right]
$$
$$
A = \frac{S_U – S_L}{\displaystyle{1 – \exp\left( \alpha L \right)}}
\raise{-12px}{,} \quad
B = \frac{\displaystyle{S_L – S_U \exp\left( \alpha L \right)}}{\displaystyle{{1 – \exp\left( \alpha L \right)}}}
\raise{-12px}{,} \quad
D = \frac{k_s}{\alpha(\theta_s – \theta_r)}
$$
で与えられます。
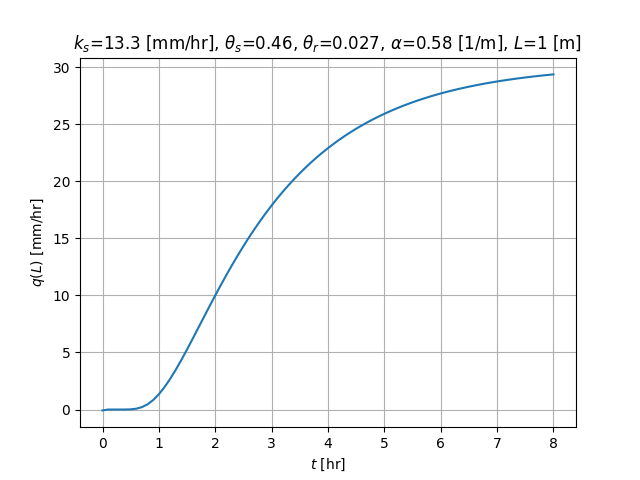
これを Python で書いて(\(\infty\) は 500 で置換)、\(S_U=1\)、\(S_L=0\)、\(S_0(z)=0\) の元で \(z = L\) における流量の時間分布を計算した結果が下図です。論文に掲載されている図と一致しています。
上式の導出にあたっては、変数変換、変数分離法、フーリエ級数展開といった聞き覚えのある手法がエレガントに用いられています。
大学の専門過程ではこういった技を一通り習得した事を前提として講義するのが建前となっていますが、大抵は何に使うのか分かっていないので、この建前が成立していないのが実態です。もっとも、それより単位をとるのに必死 org
専門過程でも使途に応じたフォローアップがあったなら有益なのになぁ~、とつくづく思います。こんな年寄りが「スバラシー」と思っても明らかに時すでに遅しです。