途中に円柱が存在する水平床の水路を考える。
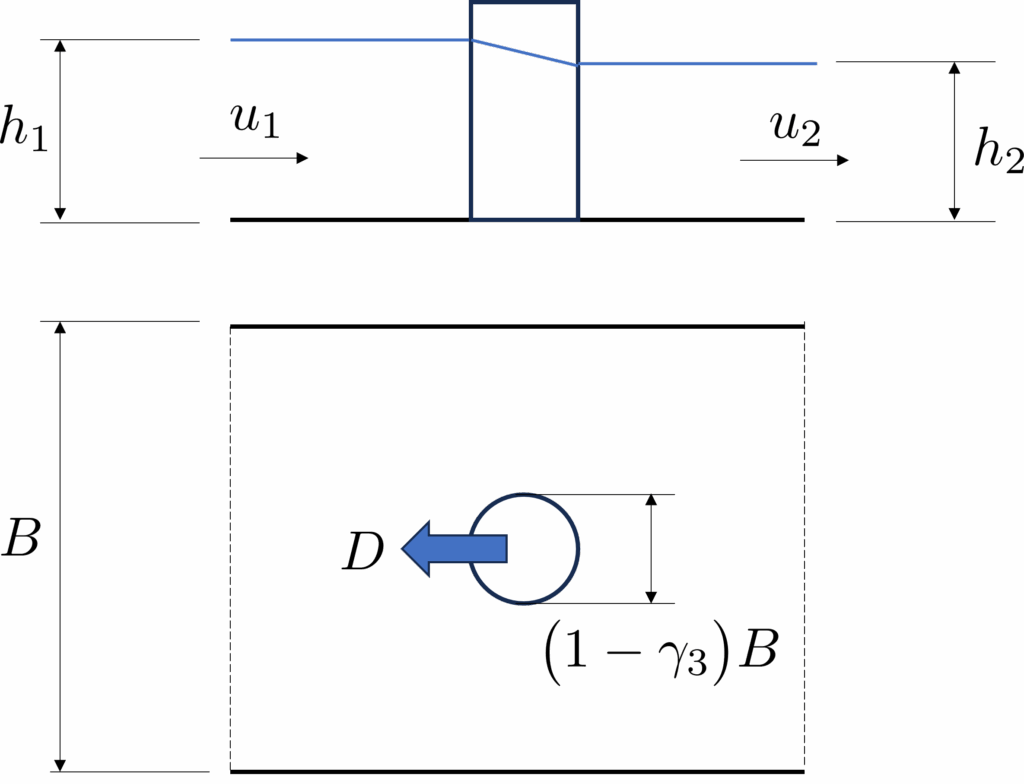
定常流を仮定して運動量の保存を考えると
$$
\frac{\rho h_1^2}{2} \,\gamma_1 B – \frac{\rho h_2^2}{2} \, \gamma_2 B – D =
u_2^2 \cdot \gamma_2 B h_2 – u_1^2 \cdot \gamma_1 B h_1
\quad \bigl(\gamma_1 = \gamma_2 = 1 \bigr)
$$
導出に際しては静水圧分布を仮定して底面摩擦を無視した。\(D\) は抗力で
$$
D = C_D \bigl(1 – \gamma_3) B h_1 \frac{\rho u_1^2}{2}
$$
したがって、何れか片方の流速・水深を与えて、連続式(\( u_1 h_1 = u_2 h_2\))と連立するとこの式は解ける。
さて、ここで上図の区間を円柱の中央で分断すると
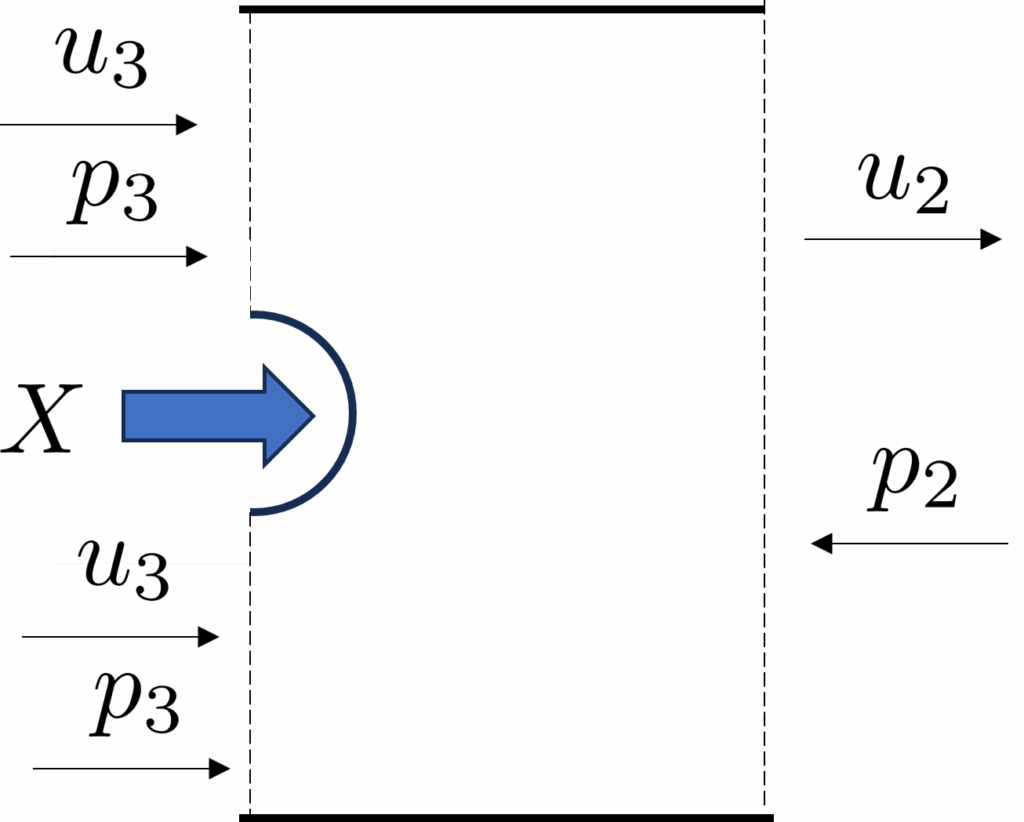
運動量の保存は
$$
\frac{\rho h_3^2}{2} \,\gamma_3 B – \frac{\rho h_2^2}{2} \, \gamma_2 B + X =
u_2^2 \cdot \gamma_2 B h_2 – u_3^2 \cdot \gamma_3 B h_3
$$
よって
$$
\Delta \left( \gamma u^2 h + \frac{\gamma \rho h^2}{2} \right)B
= X
$$
Oops ! この式は \(X\) が分からないので解けない。
と、ところが『●■▼◆マニュアル(第 4 版)』では下図の状況(セルフェースに建物)でも冒頭の図に対応する
$$
\Delta \left( \gamma u^2 h + \frac{\gamma \rho h^2}{2} \right)B
= -D
$$
が適用される。「マニュアル準拠」をうたって高額なアプリケーションが販売されてるけど大丈夫?
ちなみに昔のマニュアルでは「透過率」なる妙なパラメータがなくてマトモだったのだが・・・