今回は下図のように matplotlib で latex を使うというヲタクな話題です。
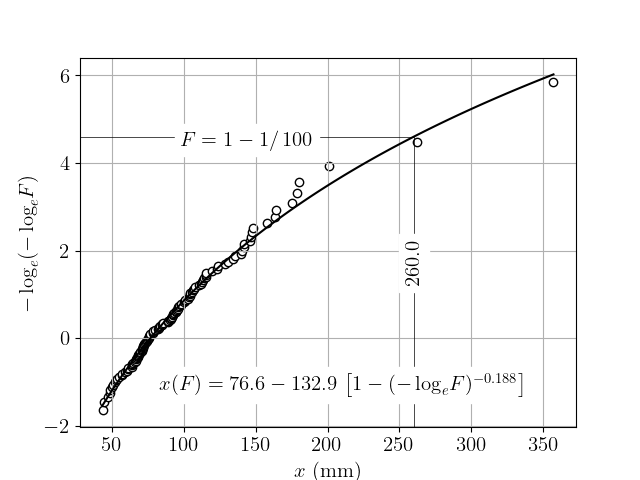
上図の描画部のコードは以下のようになっています。
def can_usetex():
path = os.environ['PATH']
paths = path.split(os.pathsep)
for p in paths:
f = os.path.join(p, 'latex.exe')
if os.path.isfile(f):
return True
return False
def show_figure():
if can_usetex():
plt.rcParams["text.usetex"] = True
plt.rcParams["text.latex.preamble"] = "\\usepackage{amsmath,bm}"
plt.rcParams["font.family"] = "serif"
plt.rcParams["font.size"] = 15
:
plt.xlabel('$x$ (mm)')
plt.ylabel('$-\\log_e(-\\log_e \\! F)$')
plt.text(x1, y1, '260.0', horizontalalignment='center',
bbox=bbox, rotation=90)
plt.text(x2, y2, '$F=1-1/100$', horizontalalignment='center',
bbox=bbox)
plt.text(x3, y3, str_formula, horizontalalignment='center',
bbox=bbox)
: サーチパス上に latex.exe が存在する(can_use 関数の戻り値が真)場合、12 ~ 15 行を加えて、matplotlib の実行環境を設定するだけです。
親和性高いですね。
ところで、水文量の頻度分析では色んな分布関数を想定して・・・というのが業界のルールになっていますが、標本数が大数になると、極値分布は Gumbel 分布、Fŕchet分布、負の Weibull 分布の何れかに収束する(Fisher-Tippett-Gnedenko theorem この記事が興味深い)というのが極値理論の教えるところです。
なので、限られた標本数で実績分布と想定した分布関数の適合度を相互に比較することにさほど意味が無いように思います(合っているに越したことはないが・・・)。上の 3 分布を組み合わせた一般化極値分布(GEV)一択で良いのではないでしょうか?
その他、業界ルールに関しては S▲★C の使用とか、(母数ではなく)クオンタイルのリサンプリングとかも違和感があります。他分野の統計分析では決して耳にしません。
以上、matplotlib + latex に事寄せて、現行の水文統計の批評になってしまいました。